Advertisements
Advertisements
प्रश्न
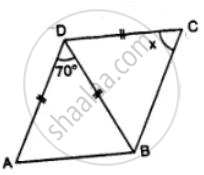
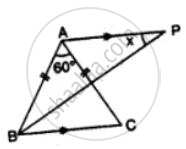
Find x in Figure Given: DA = DB = DC, BD bisects ∠ABC and∠ADB = 70°.
उत्तर
In the figure,
DA = DB = DC
BD bisects ∠ABC
and ∠ADB = 70°

But ∠ADB + ∠DAB + ∠DBA = 180° ............(Angles of a triangle)
⇒ 70° + ∠DBA + ∠DBA = 180° ........(∵ DA = DB)
⇒ 70° + 2 ∠DBA = 180°
⇒ 2 ∠DBA = 180° − 70°
= 110°
∴ ∠DBA =`(110°)/2=55°`
∵ BD is the bisector of ∠ABC,
∴ ∠DBA = ∠DBC = 55°
But in Δ DBC,
DB = DC
∴ ∠DCB = ∠DBC
⇒ x = 55°
APPEARS IN
संबंधित प्रश्न
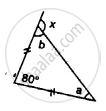
Find the unknown angles in the given figure:
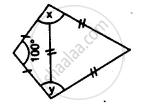
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
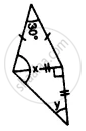
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
The base angle of an isosceles triangle is 15° more than its vertical angle. Find its each angle.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1: 4. Find each angle of the triangle.
In Figure, BP bisects ∠ABC and AB = AC. Find x.
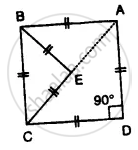
In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠ABE

In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠BAE
In the figure, AB is parallel to CD, find x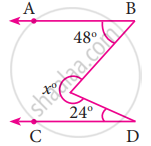
The angles of a triangle are in the ratio 1 : 2 : 3, find the measure of each angle of the triangle
