Question

In the given figure, show that: ∠a = ∠b + ∠c

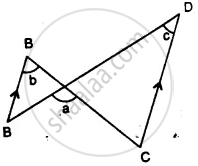
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.

Answer 1

∵ AB || CD

∴ b = c and ∠A = ∠C ........(Alternate angles)

Now in Δ PCD,

Ext. ∠APC = ∠C + ∠D

⇒ a = b + c

(i) If b = 60°, c = 50°, then

a = b + c = 60° + 50° = 110°

(ii) If a = 100° and b = 55°,

then a = b + c

⇒ 100° = 55°+ c

⇒ c = 100°− 55° = 45°

(iii) If a = 108° and c = 48°

then a = b + c

⇒ 108° = b + 48°

⇒ b = 108°− 48° = 60°