Advertisements
Advertisements
Question
Is the following statement true and false :
If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
Options
Ture
False
Solution
If one angle of a triangle is obtuse, then it cannot be a right angles triangle.
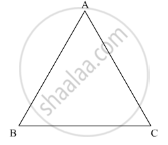
According to the angle sum property of the triangle
In ΔABC
∠A +∠B + ∠C = 180°
Now, if it is a right angled triangle
Then,
∠A + ∠B + ∠C = 180°
90° + ∠B + ∠C =180°
∠B +∠C = 90°
Also if one of the angle’s is obtuse
∠B +∠C > 90°
This is not possible.
Thus, if one angle of a triangle is obtuse, then it cannot be a right angled triangle.
APPEARS IN
RELATED QUESTIONS
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
Can a triangle have two right angles? Justify your answer in case.
Can a triangle have All angles less than 60° Justify your answer in case.
Can a triangle have All angles equal to 60°? Justify your answer in case.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Define a triangle.
Can a triangle together have the following angles?
55°, 55° and 80°
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.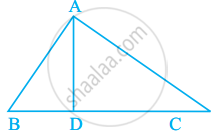
Can we have two acute angles whose sum is an obtuse angle? Why or why not?
