Advertisements
Advertisements
Question
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
Advertisements
Solution
Given,
In ΔABC
∠ABC=∠ ACB
Divide both sides by '2'
`1/2∠ABC=1/2∠ACB`
⇒ ∠OBC=∠ OCB [∵ OB, OC bisects ∠B and ∠C]
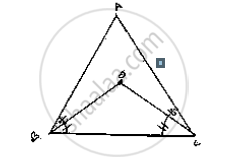
Now
`∠BOC=90^@+1/2∠A`
`120^@-90^@=1/2∠A`
`30^@xx(2)=∠A`
`∠A=60^@`
Now in Δ ABC
`∠A+∠ABC+∠ACB=180^@` (Sum of all angles of a triangle)
[∵∠ABC=∠ACB]
`60^@+2∠ABC=180^@`
`2∠ABC=180^@-60^2`
`∠ABC=120^@/2=90^@`
`∠ABC=∠ ACB`
`∴ ∠ACB=60^@`
Hence proved.
APPEARS IN
RELATED QUESTIONS
Is the following statement true and false :
A triangle can have two obtuse angles.
If two acute angles of a right triangle are equal, then each acute is equal to
In ΔABC, ∠B = ∠C and ray AX bisects the exterior angle ∠DAC. If ∠DAX = 70°, then ∠ACB =
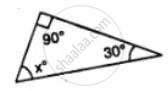
Calculate the unknown marked angles of the following figure :
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.
D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.
In the following figure, AD is the bisector of ∠BAC. Prove that AB > BD.
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
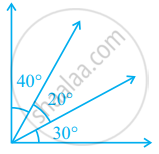
Can we have two acute angles whose sum is an acute angle? Why or why not?
