Advertisements
Advertisements
प्रश्न
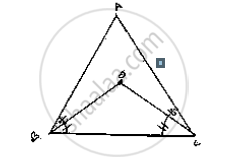
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
उत्तर
Given,
In ΔABC
∠ABC=∠ ACB
Divide both sides by '2'
`1/2∠ABC=1/2∠ACB`
⇒ ∠OBC=∠ OCB [∵ OB, OC bisects ∠B and ∠C]
Now
`∠BOC=90^@+1/2∠A`
`120^@-90^@=1/2∠A`
`30^@xx(2)=∠A`
`∠A=60^@`
Now in Δ ABC
`∠A+∠ABC+∠ACB=180^@` (Sum of all angles of a triangle)
[∵∠ABC=∠ACB]
`60^@+2∠ABC=180^@`
`2∠ABC=180^@-60^2`
`∠ABC=120^@/2=90^@`
`∠ABC=∠ ACB`
`∴ ∠ACB=60^@`
Hence proved.
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
Is the following statement true and false :
A triangle can have two right angles.
Is the following statement true and false :
An exterior angle of a triangle is less than either of its interior opposite angles.
State exterior angle theorem.
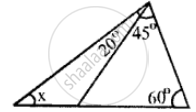
Find the unknown marked angles in the given figure:
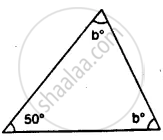
In the following, find the marked unknown angle:
Classify the following triangle according to sides:
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.