Advertisements
Advertisements
प्रश्न
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
उत्तर
Given,
In ΔABC
∠ABC=∠ ACB
Divide both sides by '2'
`1/2∠ABC=1/2∠ACB`
⇒ ∠OBC=∠ OCB [∵ OB, OC bisects ∠B and ∠C]
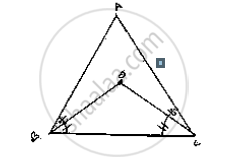
Now
`∠BOC=90^@+1/2∠A`
`120^@-90^@=1/2∠A`
`30^@xx(2)=∠A`
`∠A=60^@`
Now in Δ ABC
`∠A+∠ABC+∠ACB=180^@` (Sum of all angles of a triangle)
[∵∠ABC=∠ACB]
`60^@+2∠ABC=180^@`
`2∠ABC=180^@-60^2`
`∠ABC=120^@/2=90^@`
`∠ABC=∠ ACB`
`∴ ∠ACB=60^@`
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which ∠A — 72°, the internal bisectors of angles B and C meet in O.
Find the magnitude of ∠BOC.
Can a triangle have two acute angles?Justify your answer in case.
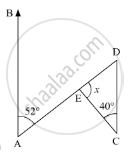
Compute the value of x in the following figure:
Is the following statement true and false :
All the angles of a triangle can be equal to 60°.
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
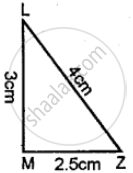
Classify the following triangle according to sides:
The correct statement out of the following is 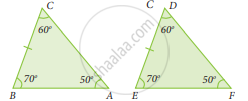
In the following figure, AD is the bisector of ∠BAC. Prove that AB > BD.
Can we have two acute angles whose sum is a straight angle? Why or why not?
Jincy used these shapes to make drawings of fish.

Now you also use some shapes to draw the different sea animals shown below.

Sea urchin

Lobster

Eel

Red snapper

Octopus

Clam

Parrotfish

Prawn

Cuttlefish

Jellyfish

Squid

Silver pomfret

Crab
