Advertisements
Advertisements
प्रश्न
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
उत्तर
Given each angle of a triangle less than the sum of the other two
`∴∠A+∠ B+∠C`
`⇒∠A+∠A<∠A+∠B+∠C`
`⇒2∠A<180^@`
[Sum of all angles of a triangle]
`⇒∠A<90^@`
Similarly` ∠ B< 90^@ and ∠C<90^@`
Hence, the triangles acute angled.
APPEARS IN
संबंधित प्रश्न
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angle is 55°, then the measure of the other interior angle is
Calculate the angles of a triangle if they are in the ratio 4: 5: 6.
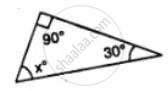
Calculate the unknown marked angles of the following figure :
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
The length of the sides of the triangle is given. Say what types of triangles they are 4.3 cm, 4.3 cm, 4.3 cm.
The length of the sides of the triangle is given. Say what types of triangles they are 3.7 cm, 3.4 cm, 4 cm.
In a ∆ABC, AB = AC. The value of x is ________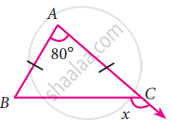
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
