Advertisements
Advertisements
प्रश्न
The exterior angles, obtained on producing the base of a triangle both way are 104° and 136°. Find all the angles of the triangle.
उत्तर
In the given problem, the exterior angles obtained on producing the base of a triangle both ways are 104°and .136° So, let us draw ΔABC and extend the base BC, such that:
∠ACD = 104°
∠ABE = 136°
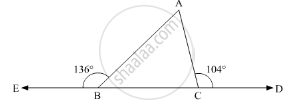
Here, we need to find all the three angles of the triangle.
Now, since BCD is a straight line, using the property, “angles forming a linear pair are supplementary”, we get
∠ACB + ∠ADC = 180°
∠ACB + 104° = 180°
∠ACB = 180° - 104°
∠ACB = 76°
Similarly, EBC is a straight line, so we get,
∠ABC + ∠ABE = 180°
∠ABC + 136° = 180°
∠ABC = 44
Further, using angle sum property in ΔABC
∠ABC +∠ACB + ∠BAC = 180°
44 + 76 + ∠BAC = 180°
∠ABC = 180° - 120°
∠ABC = 60°
Therefore,∠ACB = 76°, ∠BAC = 60°, ∠ABC = 44°.
APPEARS IN
संबंधित प्रश्न
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Is the following statement true and false :
A triangle can have two right angles.
If the side BC of ΔABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
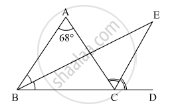
In the given figure, side BC of ΔABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
If the angles of a triangle are equal, find its angles.
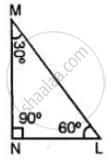
Classify the following triangle according to angle:
Find all the three angles of the ΔABC
In the given figure, AB is parallel to CD. Then the value of b is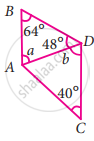
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
