Advertisements
Advertisements
प्रश्न
The exterior angles, obtained on producing the base of a triangle both way are 104° and 136°. Find all the angles of the triangle.
उत्तर
In the given problem, the exterior angles obtained on producing the base of a triangle both ways are 104°and .136° So, let us draw ΔABC and extend the base BC, such that:
∠ACD = 104°
∠ABE = 136°
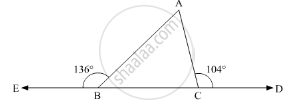
Here, we need to find all the three angles of the triangle.
Now, since BCD is a straight line, using the property, “angles forming a linear pair are supplementary”, we get
∠ACB + ∠ADC = 180°
∠ACB + 104° = 180°
∠ACB = 180° - 104°
∠ACB = 76°
Similarly, EBC is a straight line, so we get,
∠ABC + ∠ABE = 180°
∠ABC + 136° = 180°
∠ABC = 44
Further, using angle sum property in ΔABC
∠ABC +∠ACB + ∠BAC = 180°
44 + 76 + ∠BAC = 180°
∠ABC = 180° - 120°
∠ABC = 60°
Therefore,∠ACB = 76°, ∠BAC = 60°, ∠ABC = 44°.
APPEARS IN
संबंधित प्रश्न
State, if the triangle is possible with the following angles :
20°, 70°, and 90°
One angle of a right-angled triangle is 70°. Find the other acute angle.
The length of the sides of the triangle is given. Say what types of triangles they are 3 cm, 4 cm, 5 cm.
The length of the sides of the triangle is given. Say what types of triangles they are 3.7 cm, 3.4 cm, 4 cm.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
9 cm, 6 cm, 16 cm
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
12 cm, 12 cm, 16 cm
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
In the following figure, AD is the bisector of ∠BAC. Prove that AB > BD.
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
In figure, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is ______.