Advertisements
Advertisements
प्रश्न
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
उत्तर
In the given ΔABC, ∠ACD = 105°and ∠EAF = 45°. We need to find ∠ABC, ∠ACB, and ∠BAC.
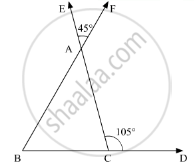
Here, ∠EAF and ∠BAC are vertically opposite angles. So, using the property, “vertically opposite angles are equal”, we get,
∠EAF = ∠BAC
∠BAC = 45°
Further, BCD is a straight line. So, using linear pair property, we get,
∠ACB + ∠ACD = 180°
∠ACB + 105° = 180°
∠ACB = 180° - 105°
∠ACB = 75°
Now, in ΔABC, using “the angle sum property”, we get,
∠ABC + ∠ACB + ∠BAC = 180°
45° + 75° + ∠ABC = 180°
∠BAC = 180°
∠BAC = 180° - 120°
∠BAC = 60
Therefore,∠ACB = 75° , ∠BAC = 45°,∠ABC = 60°.
APPEARS IN
संबंधित प्रश्न
Show that the angles of an equilateral triangle are 60° each.
The vertical angle of an isosceles triangle is 100°. Find its base angles.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
Which of the following correctly describes the given triangle?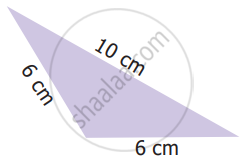
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
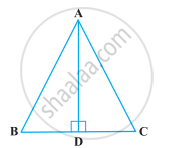
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
