Advertisements
Advertisements
प्रश्न
Which of the following correctly describes the given triangle?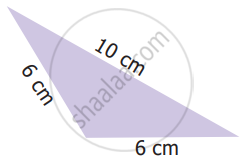
पर्याय
It is a right isosceles triangle
It is an acute isosceles triangle
It is an obtuse isosceles triangle
It is an obtuse scalene triangle.
उत्तर
It is an obtuse isosceles triangle
APPEARS IN
संबंधित प्रश्न
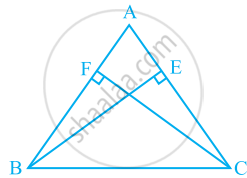
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Which of the following statements are true (T) and which are false (F)?
Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
If the measures of angles of a triangle are in the ratio of 3 : 4 : 5, what is the measure of the smallest angle of the triangle?
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
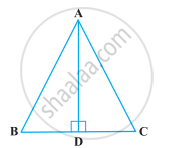
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
