Advertisements
Advertisements
प्रश्न
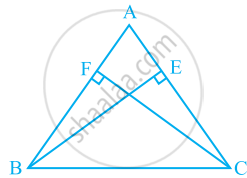
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
उत्तर
△ABC is an isosceles triangle.
∴ AB = AC
∠ACB = ∠ABC ...[Angles opposite to equal sides of a △ are equal]
∠BCE = ∠CBF
Now, in △BEC and △CFB
∠BCE = ∠CBF ...[Proved above]
∠BEC = ∠CFB ...[Each 90°]
BC = CB ...[Common]
∴ △BEC ≅ △CFB ...[By AAS congruence]
So, BE = CF ...[By Corresponding parts of congruent triangles]
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
Which of the following statements are true (T) and which are false (F):
Sides opposite to equal angles of a triangle may be unequal
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
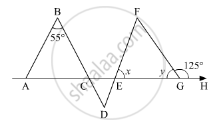
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
In ∆PQR, if ∠R > ∠Q, then ______.
