Advertisements
Advertisements
प्रश्न
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

उत्तर
i. In △ABE and △ACF, we have
∠AEB = ∠AFC ...[Each = 90° as BE ⊥ AC and CF ⊥ AB]
∠A = ∠A ...[Common]
BE = CF ...[Given]
∴ △ABE ≌ △ACF ...[By AAS congruence rule]
ii. Since, △ABE ≌ △ACF
∴ AB = AC ...[By Corresponding parts of congruent triangles]
⇒ ABC is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
Show that the angles of an equilateral triangle are 60° each.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
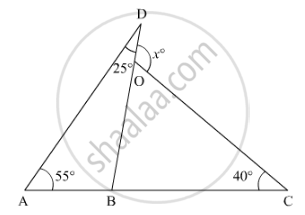
In the given figure, the value of x is ______.
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
