Advertisements
Advertisements
प्रश्न
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
उत्तर
In triangle ABD,
AB + BD > AD ...(i)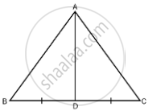
AC + CD > AD ...(ii) [Sum of the length of any two sides of a triangle must be greater must be greater that the third side]
Adding (i) and (ii), we get
AB + BD + CD + AC > 2AD
AB + BC + CA > 2AD ...[BD = CD as AD is median of triangle ABC]
APPEARS IN
संबंधित प्रश्न
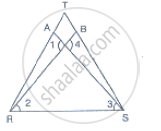
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
The vertical angle of an isosceles triangle is 100°. Find its base angles.
Prove that each angle of an equilateral triangle is 60°.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
Fill the blank in the following so that the following statement is true.
In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
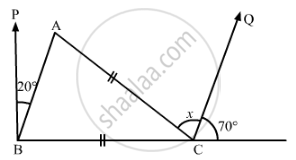
In the given figure, if BP || CQ and AC = BC, then the measure of x is
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
