Advertisements
Advertisements
प्रश्न
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
उत्तर
False (F)
Reason: The angular bisector of the vertex angle is also a median
⇒ The triangle must be an isosceles and also may be an equilateral triangle.
APPEARS IN
संबंधित प्रश्न
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
Fill the blank in the following so that the following statement is true.
If altitudes CE and BF of a triangle ABC are equal, then AB = ....
Which of the following statements are true (T) and which are false (F)?
Difference of any two sides of a triangle is equal to the third side.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
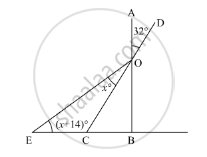
In the given figure, if AB ⊥ BC. then x =
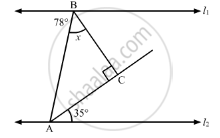
In the given figure, for which value of x is l1 || l2?
In ∆PQR, if ∠R > ∠Q, then ______.
M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
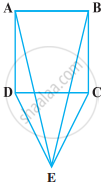
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.