Advertisements
Advertisements
प्रश्न
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
उत्तर
False (F)
Reason: The angular bisector of the vertex angle is also a median
⇒ The triangle must be an isosceles and also may be an equilateral triangle.
APPEARS IN
संबंधित प्रश्न
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
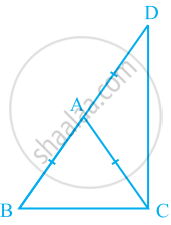
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
Which of the following statements are true (T) and which are false (F):
Angles opposite to equal sides of a triangle are equal
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
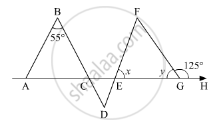
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In the given figure, what is y in terms of x?

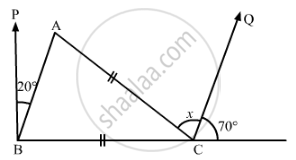
In the given figure, if BP || CQ and AC = BC, then the measure of x is
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
