Advertisements
Advertisements
प्रश्न
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
उत्तर
False (F)
Reason: Since two sides are equal, the triangle is an isosceles triangle.
⇒ The two altitudes corresponding to two equal sides must be equal.
APPEARS IN
संबंधित प्रश्न
Find the measure of each exterior angle of an equilateral triangle.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Find the measure of each exterior angle of an equilateral triangle.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
Fill the blank in the following so that the following statement is true.
In a ΔABC if ∠A = ∠C , then AB = ......
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
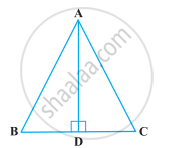
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
