Advertisements
Advertisements
प्रश्न
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
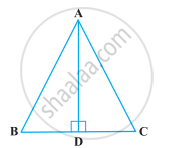
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
उत्तर
In ∆ABC, AB = AC
⇒ ∠ACB = ∠ABC ...[Angles opposite to the equal sides are equal]
In ∆ABD and ∆ACD,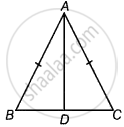
AB = AC ...[Given]
∠ABD = ∠ACD ...[Proved above]
∠ADB = ∠ADC ...[Each 90°]
∴ ∆ABD ≅ ∆ACD ...[By AAS]
So, ∠BAD = ∠CAD ...[By CPCT]
So, the defect in the given argument is that firstly prove ∠ABD = ∠ACD
Hence, ∠ABD = ∠ACD is defect.
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
The angles of a right angled triangle are
In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
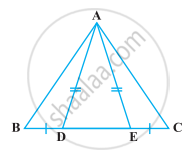
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
