Advertisements
Advertisements
प्रश्न
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
उत्तर
Let ΔABC be isosceles such that AB = AC
⇒∠B=∠C
Given that vertex angle A is twice the sum of the base angles B and C.
i.e., ∠A=2(∠B+∠C)
⇒∠A=2(∠B+∠B) [∵∠B=∠C]
⇒∠A=2(2∠B)
⇒∠A=4∠B
Now,
We know that sum of angles in a triangle 180°
⇒ ∠A+ ∠B+ ∠C=180°
4∠B+∠B+∠B=180° [∵∠A=4∠B and ∠B=∠C]
6∠B=180°
`∠B=(180°) /6=30° ` ∠B=30°
Since, ∠B=∠C⇒ ∠B=∠C=30°
And` ∠A=4∠B⇒ ∠A=4xx30°=120° `
∴Angles of the given triangle are 120°,30°,30°

APPEARS IN
संबंधित प्रश्न
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
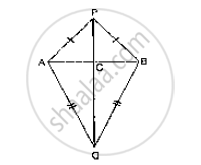
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
Fill the blank in the following so that the following statement is true.
In a ΔABC if ∠A = ∠C , then AB = ......
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
Which of the following statements are true (T) and which are false (F)?
Sum of the three sides of a triangle is less than the sum of its three altitudes.
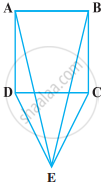
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
Find all the angles of an equilateral triangle.
