Advertisements
Advertisements
Question
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
Solution
Let ΔABC be isosceles such that AB = AC
⇒∠B=∠C
Given that vertex angle A is twice the sum of the base angles B and C.
i.e., ∠A=2(∠B+∠C)
⇒∠A=2(∠B+∠B) [∵∠B=∠C]
⇒∠A=2(2∠B)
⇒∠A=4∠B
Now,
We know that sum of angles in a triangle 180°
⇒ ∠A+ ∠B+ ∠C=180°
4∠B+∠B+∠B=180° [∵∠A=4∠B and ∠B=∠C]
6∠B=180°
`∠B=(180°) /6=30° ` ∠B=30°
Since, ∠B=∠C⇒ ∠B=∠C=30°
And` ∠A=4∠B⇒ ∠A=4xx30°=120° `
∴Angles of the given triangle are 120°,30°,30°

APPEARS IN
RELATED QUESTIONS
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Which of the following statements are true (T) and which are false (F):
Sides opposite to equal angles of a triangle may be unequal
Which of the following statements are true (T) and which are false (F):
The bisectors of two equal angles of a triangle are equal
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
In the given figure, what is the value of x?
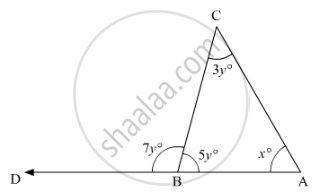
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
