Advertisements
Advertisements
Question
In the given figure, what is the value of x?
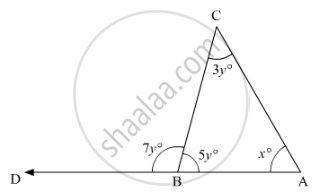
Options
35
45
50
60
Solution
In the given figure, we need to find the value of x.
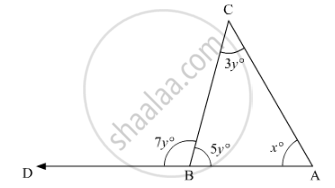
Here, DBA is a straight line, so using the property, “angles forming a linear pair are supplementary”, we get,
∠CBA + ∠CBD = 180°
7y + 5y = 180°
12y = 180°
`y = (180°)/12`
y = 15°
Now, applying the value of y in ∠CBA and ∠BCA
∠BCA = 3y
= 3(15°)
= 45°
Also,
∠CBA = 5y
= 5(15°)
= 75°
Further, applying angle sum property of the triangle
In ΔABC
∠A + ∠B +∠C = 180°
x + 75° + 45° = 180°
x + 120°= 180°
x = 180° - 120°
x = 60°
Thus, x = 60°
APPEARS IN
RELATED QUESTIONS
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
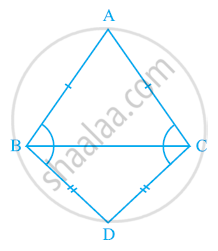
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
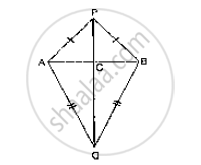
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
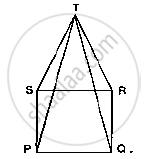
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
Prove that the medians of an equilateral triangle are equal.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
Which of the following statements are true (T) and which are false (F):
The bisectors of two equal angles of a triangle are equal
The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ______.
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
