Advertisements
Advertisements
Question
Prove that the medians of an equilateral triangle are equal.
Solution
Given to prove that the medians of an equilateral triangle are equal
Median: The line joining the vertex and midpoint of opposite side.
Now, consider an equilateral triangle ABC
Let D,E,F are midpoints of , BC CAand . AB
Then, , AD BE and CF are medians of . Δ ABC
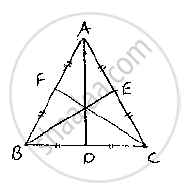
Now ,
D is midpoint of BC⇒ BD = DC =`(BC)/2`
Similarly ,` CE=EA=(AC)/2`
`AF= FB=(AB)/2`
Since Δ ABC is an equilateral traingle ⇒ AB=BC= CA .............(1)
`BD=DC=CE=EA=AF=FB= (BC)/2=(AC)/2 (AB)/2` ..............(2)
And also , ∠ ABC= ∠ BCA=∠CAB=60° ..................(3)
Now, consider Δ ABD and Δ BCE
AB=BC [from (1)]
BD= CE [from (2)]
∠ ABD= ∠ BCE [from (3)] [∠ ABD and ∠ ABC and ∠ BCE and BCA aare same ]
So, from SAS congruence criterion , we have
Δ ABD ≅ Δ BCE
AD= BE ........................(4)
[corresponding parts of congruent triangles are equal]
Now, consider ΔBCE and Δ CAF,
BC = CA [from (1)]
∠BCE =∠ CAF [from (3)]
[∠ BCE and ∠ BCA and ∠ CAF annd ∠ CAB are same ]
CE=AF [from (2)]
So, from SAS congruence criterion, we have Δ BCE≅ Δ CAF
⇒ BE=CF ..........................(5)
[Corresponding parts of congruent triangles are equal ]
From (4) and (5), we have
AD =BE= CF
⇒Median AD = Median BE = Median CF
∴The medians of an equilateral triangle are equal
∴Hence proved
APPEARS IN
RELATED QUESTIONS
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
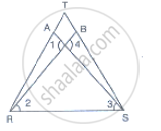
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
Fill in the blank to make the following statement true.
In a right triangle the hypotenuse is the .... side.
In the given figure, what is z in terms of x and y?
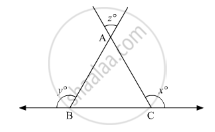
In the given figure, for which value of x is l1 || l2?
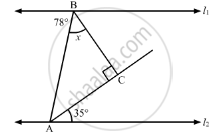
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
Find all the angles of an equilateral triangle.
