Advertisements
Advertisements
Question
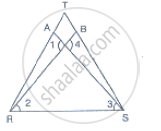
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
Solution
In the figure given that
RT = TS ……..(1)
∠1 = 2∠2 ……..(2)
And∠4 = `2sqrt` ................(3)
And given to prove ΔRBT≅ ΔSAT
Let the point of intersection of RB and SA be denoted by O Since RB and SA intersect at O.
∴∠AOR = ∠BOS [Vertically opposite angles]
⇒∠1 = ∠4
⇒ 2∠2 = 2∠3 [From (2) and (3)
Þ
Þ ∠2 = ∠3 ……..(4)
Now we have RT = TS ∠∠TRS
∴ΔTRS is an isosceles triangle
∴∠TRS = ∠TSR ……..(5) [Angles opposite to equal sides are equal]
But we have
∠TRS = ∠TRB + ∠2 ………(6)
And ∠TSR = ∠TSA + ∠3 ……….(7)
Putting (6) and (7) in (5) we get
∠TRB +∠2 = ∠TSA + ∠B
⇒∠ TRB =∠TSA [∵ From (4)]
Now considerΔRBT and ΔSAT
RT = ST [From (1)]
∠TRB = ∠TSA [From (4)]
∠RTB =∠ STA [Common angle]
From ASA criterion of congruence, we have ΔRBT ≅ΔSAT
APPEARS IN
RELATED QUESTIONS
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
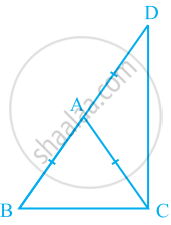
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
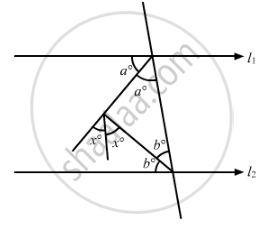
In the given figure, if l1 || l2, the value of x is