Advertisements
Advertisements
Question
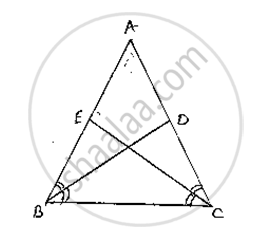
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
Solution
Given that ΔABC is isosceles with AB = AC and BD and CE are bisectors of ∠B and ∠C
We have to prove BD = CE
Since AB = AC ⇒ ∠ABC = ∠ACB …….(1)
[∵ Angles opposite to equal sides are equal]
Since BD and CE are bisectors of ∠B and ∠C
`∠ABD = ∠DBC = ∠BCE = ECA =`(∠B)/2=(∠C)/2` …….(2)
Now,
Consider ΔEBC andΔDCB
∠EBC = ∠DCB [∵ ∠B = ∠C ] from (1)
BC = BC [Common side]
∠BCE = ∠CBD [ ∵ From (2)]
So, by ASA congruence criterion, we have ΔEBC ≅ΔDCB
Now,
CE = BD [∵ Corresponding parts of congruent triangles are equal]
or BD = CE
∴Hence proved
Since AD || BC and transversal AB cuts at A and B respectively
∴∠DAO = ∠OBC ……….(2) [alternate angle]
And similarly respectively AD || BC and transversal DC cuts at D ad C respectivaly
∴ ∠ADO = ∠OCB ………(3) [alternate angle]
Since AB and CD intersect at O.
∴∠AOD = ∠BOC [Vertically opposite angles]
Now consider ΔAOD and ΔBOD
∠DAO = ∠OBC [∵ From (2)]
AD = BC [ ∵ From (1)]
And ∠ADO = ∠OCB [From (3)]
So, by ASA congruence criterion, we have
ΔAOD ≅ΔBOC
Now,
AO = OB and DO = OC [∵Corresponding parts of congruent triangles are equal]
⇒Lines AB and CD bisect at O.
∴Hence proved
APPEARS IN
RELATED QUESTIONS
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
If ΔABC ≅ ΔABC is isosceles with
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
In the given figure, AB = DB and AC = DC. Find the values of x and y.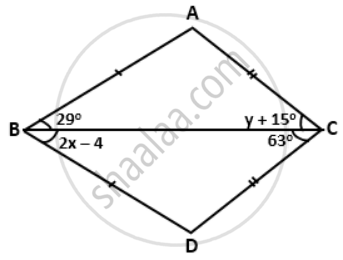
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
