Advertisements
Advertisements
प्रश्न
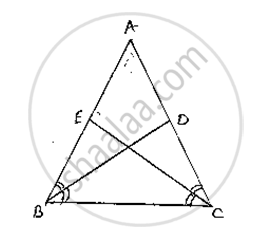
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
उत्तर
Given that ΔABC is isosceles with AB = AC and BD and CE are bisectors of ∠B and ∠C
We have to prove BD = CE
Since AB = AC ⇒ ∠ABC = ∠ACB …….(1)
[∵ Angles opposite to equal sides are equal]
Since BD and CE are bisectors of ∠B and ∠C
`∠ABD = ∠DBC = ∠BCE = ECA =`(∠B)/2=(∠C)/2` …….(2)
Now,
Consider ΔEBC andΔDCB
∠EBC = ∠DCB [∵ ∠B = ∠C ] from (1)
BC = BC [Common side]
∠BCE = ∠CBD [ ∵ From (2)]
So, by ASA congruence criterion, we have ΔEBC ≅ΔDCB
Now,
CE = BD [∵ Corresponding parts of congruent triangles are equal]
or BD = CE
∴Hence proved
Since AD || BC and transversal AB cuts at A and B respectively
∴∠DAO = ∠OBC ……….(2) [alternate angle]
And similarly respectively AD || BC and transversal DC cuts at D ad C respectivaly
∴ ∠ADO = ∠OCB ………(3) [alternate angle]
Since AB and CD intersect at O.
∴∠AOD = ∠BOC [Vertically opposite angles]
Now consider ΔAOD and ΔBOD
∠DAO = ∠OBC [∵ From (2)]
AD = BC [ ∵ From (1)]
And ∠ADO = ∠OCB [From (3)]
So, by ASA congruence criterion, we have
ΔAOD ≅ΔBOC
Now,
AO = OB and DO = OC [∵Corresponding parts of congruent triangles are equal]
⇒Lines AB and CD bisect at O.
∴Hence proved
APPEARS IN
संबंधित प्रश्न
Which of the following is not a criterion for congruence of triangles?
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
State, whether the pairs of triangles given in the following figures are congruent or not:

State, whether the pairs of triangles given in the following figures are congruent or not:
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.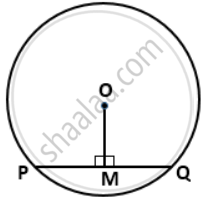
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.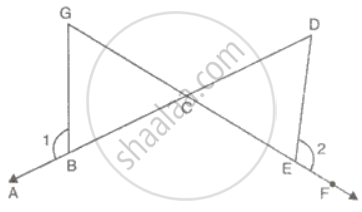
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side BC of ∆ABC so that the two triangles are congruent? Give reason for your answer.
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?
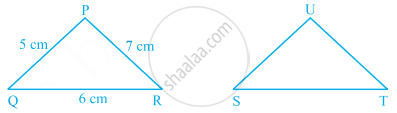
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
