Advertisements
Advertisements
प्रश्न
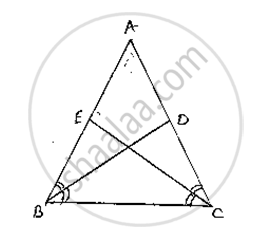
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
उत्तर
Given that ΔABC is isosceles with AB = AC and BD and CE are bisectors of ∠B and ∠C
We have to prove BD = CE
Since AB = AC ⇒ ∠ABC = ∠ACB …….(1)
[∵ Angles opposite to equal sides are equal]
Since BD and CE are bisectors of ∠B and ∠C
`∠ABD = ∠DBC = ∠BCE = ECA =`(∠B)/2=(∠C)/2` …….(2)
Now,
Consider ΔEBC andΔDCB
∠EBC = ∠DCB [∵ ∠B = ∠C ] from (1)
BC = BC [Common side]
∠BCE = ∠CBD [ ∵ From (2)]
So, by ASA congruence criterion, we have ΔEBC ≅ΔDCB
Now,
CE = BD [∵ Corresponding parts of congruent triangles are equal]
or BD = CE
∴Hence proved
Since AD || BC and transversal AB cuts at A and B respectively
∴∠DAO = ∠OBC ……….(2) [alternate angle]
And similarly respectively AD || BC and transversal DC cuts at D ad C respectivaly
∴ ∠ADO = ∠OCB ………(3) [alternate angle]
Since AB and CD intersect at O.
∴∠AOD = ∠BOC [Vertically opposite angles]
Now consider ΔAOD and ΔBOD
∠DAO = ∠OBC [∵ From (2)]
AD = BC [ ∵ From (1)]
And ∠ADO = ∠OCB [From (3)]
So, by ASA congruence criterion, we have
ΔAOD ≅ΔBOC
Now,
AO = OB and DO = OC [∵Corresponding parts of congruent triangles are equal]
⇒Lines AB and CD bisect at O.
∴Hence proved
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
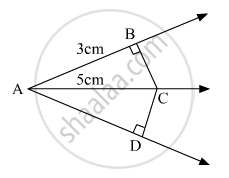
In the given figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
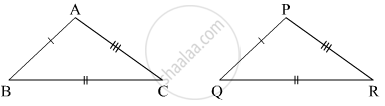
By ______ test
Δ ABC ≅ ΔPQR
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.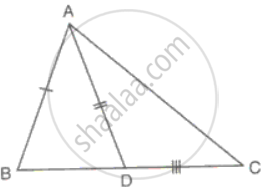
In the given figure, AB = DB and AC = DC. Find the values of x and y.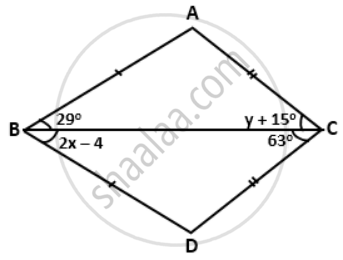
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent sides
Which of the following rule is not sufficient to verify the congruency of two triangles
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
