Advertisements
Advertisements
प्रश्न
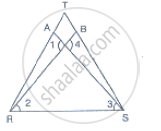
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
उत्तर
In the figure given that
RT = TS ……..(1)
∠1 = 2∠2 ……..(2)
And∠4 = `2sqrt` ................(3)
And given to prove ΔRBT≅ ΔSAT
Let the point of intersection of RB and SA be denoted by O Since RB and SA intersect at O.
∴∠AOR = ∠BOS [Vertically opposite angles]
⇒∠1 = ∠4
⇒ 2∠2 = 2∠3 [From (2) and (3)
Þ
Þ ∠2 = ∠3 ……..(4)
Now we have RT = TS ∠∠TRS
∴ΔTRS is an isosceles triangle
∴∠TRS = ∠TSR ……..(5) [Angles opposite to equal sides are equal]
But we have
∠TRS = ∠TRB + ∠2 ………(6)
And ∠TSR = ∠TSA + ∠3 ……….(7)
Putting (6) and (7) in (5) we get
∠TRB +∠2 = ∠TSA + ∠B
⇒∠ TRB =∠TSA [∵ From (4)]
Now considerΔRBT and ΔSAT
RT = ST [From (1)]
∠TRB = ∠TSA [From (4)]
∠RTB =∠ STA [Common angle]
From ASA criterion of congruence, we have ΔRBT ≅ΔSAT
APPEARS IN
संबंधित प्रश्न
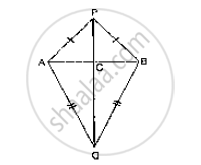
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Find the measure of each exterior angle of an equilateral triangle.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
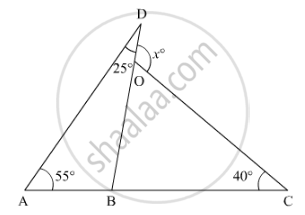
In the given figure, the value of x is ______.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
