Advertisements
Advertisements
प्रश्न
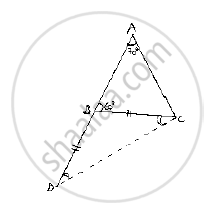
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
उत्तर
Given that in ΔABC,side AB is produced to D So that BD = BC and ∠B =60°,∠A= 70°
We have to prove that
(1)AD>CD (2)AD>AC
First join C and D
Now, in ΔABC
∠A+∠B+∠C=180° [ ∵ Sum of angles in a triangle 180° ]
⇒ ∠C=180°-70°-60°
=180°-130°=50°
∴ ∠C=50° ⇒ ∠ACB=50° ..............(1)
And also in ,Δ BDC,
∠DBC=180°-∠ABC [∵ABDis a straight angle ]
=180°-60°=120°
and also BD=BC [given]
⇒ ∠BCD=∠BDC [ ∵Angles opposite to equal sides are equal]
Now,
∠DBC+∠BCD+∠BDC=180° [ ∵Sum of angles in a triangle 180°]
⇒ 120°+∠BCD+∠BCD=180°
⇒2∠BCD=180°-120°⇒ ∠BCD=`(60°) /2=30`
∴ ∠BCD=∠BDC=30° ..............(2)
Now, consider , ΔADC,
∠BAC⇒∠DAC=70 [given]
∠BDC⇒∠ADC=30 [ ∵ From (2)]
∠ACD=∠ACB+∠BCD
=50°+ 30° [ ∵ From (1) and (2)]
=80°
Now, ∠ADC<∠DAC<ACD
⇒ AC<DC<AD
[∵ Side opposite to greater angle is longer and smaller angle is smaller]
⇒ AD>DC and AD>AC
∴Hence proved
Or
We have, ∠ACD>∠DAC and ∠ACD>∠ADC
⇒ AD>DC and AD>AC
[ ∵ Side opposite to greater angle is longer and smaller angle is smaller]
APPEARS IN
संबंधित प्रश्न
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
Fill the blank in the following so that the following statement is true.
In a ΔABC if ∠A = ∠C , then AB = ......
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
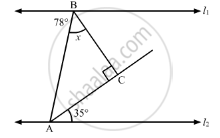
In the given figure, for which value of x is l1 || l2?
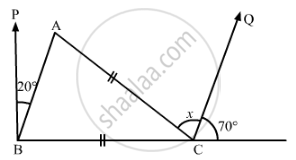
In the given figure, if BP || CQ and AC = BC, then the measure of x is
Which of the following correctly describes the given triangle?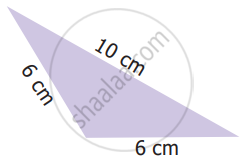
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
