Question

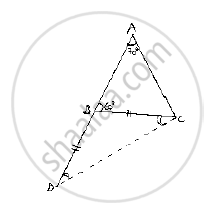
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC 

Answer 1

Given that in ΔABC,side AB is produced to D So that BD = BC and ∠B =60°,∠A= 70° 

We have to prove that 

(1)AD>CD (2)AD>AC 

First join C and D 

Now, in ΔABC 

∠A+∠B+∠C=180°           [ ∵ Sum of angles in a triangle 180° ]  

⇒ ∠C=180°-70°-60° 

=180°-130°=50° 

∴ ∠C=50° ⇒ ∠ACB=50°                 ..............(1) 

And also in ,Δ BDC, 

∠DBC=180°-∠ABC             [∵ABDis a straight angle ] 

=180°-60°=120°  

and also BD=BC          [given] 

⇒ ∠BCD=∠BDC            [ ∵Angles opposite to equal sides are equal] 

Now, 

∠DBC+∠BCD+∠BDC=180°   [ ∵Sum of angles in a triangle 180°] 

⇒ 120°+∠BCD+∠BCD=180°   

⇒2∠BCD=180°-120°⇒ ∠BCD=`(60°) /2=30` 

∴ ∠BCD=∠BDC=30°            ..............(2)

Now, consider , ΔADC, 

∠BAC⇒∠DAC=70               [given] 

∠BDC⇒∠ADC=30                [ ∵ From (2)] 

∠ACD=∠ACB+∠BCD 

=50°+ 30°                [ ∵ From (1) and (2)] 

=80° 

Now, ∠ADC<∠DAC<ACD 

⇒ AC<DC<AD 

[∵ Side opposite to greater angle is longer and smaller angle is smaller] 

⇒ AD>DC and AD>AC  

∴Hence proved 

Or
We have, ∠ACD>∠DAC and ∠ACD>∠ADC 

⇒ AD>DC  and AD>AC 

[ ∵ Side opposite to greater angle is longer and smaller angle is smaller]