Advertisements
Advertisements
प्रश्न
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
उत्तर
Given lengths of sides are 2cm, 3cm and 7cm we have to check whether it is possible to draw a triangle with ten the given lengths of sides
We know that,
A triangle can be drawn only when the sum of any two sides is greater than the third side.
So, let’s check the rule
2+3>7 or 2+3<7
2+7>3
and 3+7>2
Here, 2+3>7 So, the triangle does not exit.
APPEARS IN
संबंधित प्रश्न
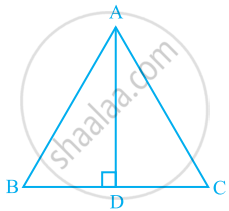
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
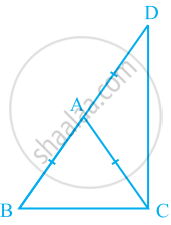
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
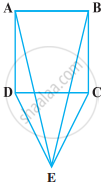
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
Write the sum of the angles of an obtuse triangle.
In ΔABC, if ∠A = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B =
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
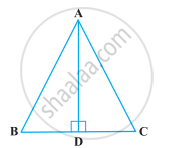
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
