Advertisements
Advertisements
प्रश्न
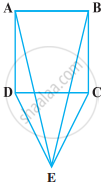
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
उत्तर
Given in figure triangle CDE is an equilateral triangle formed on a side CD of a square ABCD.
To proof that ΔADE ≅ ∆BCE
Proof: In triangle ADE and triangle BCE,
DE = CE ...[Side of an equilateral triangle]
∠ADE = ∠BCE
∠ADC = ∠BCD = 90° and ∠EDC = ∠ECD = 60°
∠ADE = 90° + 60° = 150° and ∠BCE = 90° + 60° = 150°
AD = BC ...[Sides of a square]
∆ADE ≅ ∆BCE ...[By SAS congruence rule]
APPEARS IN
संबंधित प्रश्न
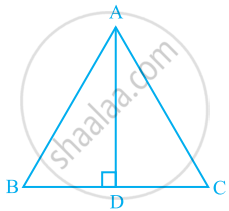
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
Show that the angles of an equilateral triangle are 60° each.
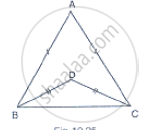
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
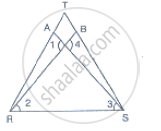
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Which of the following statements are true (T) and which are false (F):
Angles opposite to equal sides of a triangle are equal
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then

