Advertisements
Advertisements
प्रश्न
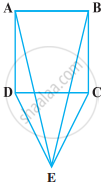
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
उत्तर
Given in figure triangle CDE is an equilateral triangle formed on a side CD of a square ABCD.
To proof that ΔADE ≅ ∆BCE
Proof: In triangle ADE and triangle BCE,
DE = CE ...[Side of an equilateral triangle]
∠ADE = ∠BCE
∠ADC = ∠BCD = 90° and ∠EDC = ∠ECD = 60°
∠ADE = 90° + 60° = 150° and ∠BCE = 90° + 60° = 150°
AD = BC ...[Sides of a square]
∆ADE ≅ ∆BCE ...[By SAS congruence rule]
APPEARS IN
संबंधित प्रश्न
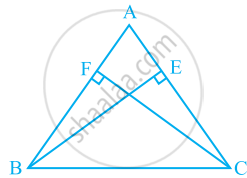
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
Fill in the blank to make the following statement true.
In a right triangle the hypotenuse is the .... side.
Fill in the blank to make the following statement true.
If two angles of a triangle are unequal, then the smaller angle has the........ side opposite to it.
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
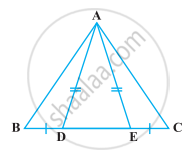
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.