Advertisements
Advertisements
प्रश्न
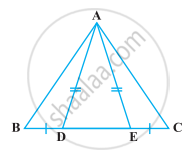
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.
उत्तर
Given: D and E are the points on side BC of a ∆ABC such that BD = CE and AD = AE.
To show: ∆ABD ≅ ∆ACE
Proof: We have, AD = AE ...[Given]
⇒ ∠ADE = ∠AED ...(i) [Since, angles opposite to equal sides are equal]
We have, ∠ADB + ∠ADE = 180° ...[Linear pair axiom]
⇒ ∠ADB = 180° – ∠ADE
= 180° – ∠AED ...[From equation (i)]
In ∆ABD and ∆ACE,
∠ADB = ∠AEC ...[∵ ∠AEC + ∠AED = 180°, linear pair axiom]
BD = CE ...[Given]
And AD = AE ...[Given]
∴ ∆ABD ≅ ∆ACE ...[By SAS congruence rule]
APPEARS IN
संबंधित प्रश्न
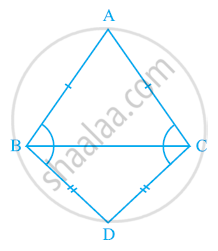
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
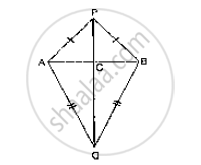
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
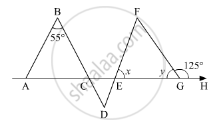
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then

If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
