Advertisements
Advertisements
प्रश्न
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
उत्तर
Yes, if ΔPQR ≅ ΔEDF, then it means that corresponding angles and their sides are equal because we know that, two triangles are congruent, if the sides and angles of one triangle are equal to the corresponding sides and angles of other triangle.
Here, ΔPQR ≅ ΔEDF
∴ PQ = ED, QR = DF and PR = EF
Hence, it is true to say that PR = EF.
APPEARS IN
संबंधित प्रश्न
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
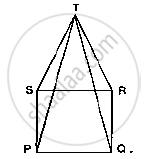
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
The vertical angle of an isosceles triangle is 100°. Find its base angles.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Fill in the blank to make the following statement true.
In a right triangle the hypotenuse is the .... side.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In the given figure, x + y =

In the given figure, what is y in terms of x?

In the given figure, if BP || CQ and AC = BC, then the measure of x is
In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then

