Advertisements
Advertisements
प्रश्न
In the given figure, x + y =

विकल्प
270
230
210
190°
उत्तर
In the given figure, we need to find x+ y
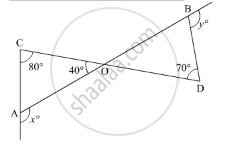
Here, AB and CD are straight lines intersecting at point O, so using the property, “vertically opposite angles are equal”, we get,
∠BOD = ∠AOC
∠BOD = 40°
Further, applying the property, “an exterior angle of a triangle is equal to the sum of the two opposite interior angles”, in ΔAOC, we get,
x° = ∠ACO + ∠AOC
x° = 80° + 40°
x° = 120°
Similarly, in ΔBOD
y° = ∠BOD + ∠BDO
y° = 40° + 70°
y° = 110°
Thus,
x° + y° = 120° + 110°
x° + y° = 230°
APPEARS IN
संबंधित प्रश्न
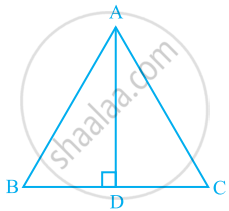
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Write the sum of the angles of an obtuse triangle.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In the given figure, what is the value of x?
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
