Advertisements
Advertisements
प्रश्न
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
उत्तर
Given: ABCD is a quadrilateral.
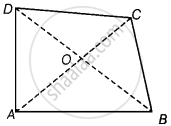
To show: AB + BC + CD + DA < 2(BD + AC)
Construction: Join diagonals AC and BD.
Proof: In ΔOAB, OA + OB > AB ...(i) [Sum of two sides of a triangle is greater than the third side]
In ΔOBC, OB + OC > BC ...(ii) [Sum of two sides of a triangle is greater than the third side]
In ΔOCD, OC + OD > CD ...(iii) [Sum of two sides of a triangle is greater than the third side]
In ΔODA, OD + OA > DA ...(iv) [Sum of two sides of a triangle is greater than the third side]
On adding equations (i), (ii), (iii) and (iv), we get
2[(OA + OB + OC + OD] > AB + BC + CD + DA
⇒ 2[(OA + OC) + (OB + OD)] > AB + BC + CD + DA
⇒ 2(AC + BD) > AB + BC + CD + DA ...[∵ OA + OC = AC and OB + OD = BD]
⇒ AB + BC + CD + DA < 2(BD + AC)
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
Which of the following statements are true (T) and which are false (F)?
Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
Which of the following correctly describes the given triangle?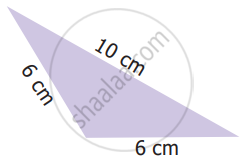
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC
