Advertisements
Advertisements
प्रश्न
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
विकल्प
100°
80°
90°
135°
उत्तर
In the given problem, line segment AB and CD intersect at O, such that ,AC || DB , ∠CAB = 45° and ∠CDB = 55° .
We need to find ∠BOD

As AC || DB
Applying the property, “alternate interior angles are equal”, we get,
∠OBD = ∠CAB
∠OBD= 55° .......(1)
Now, using the angle sum property of the triangle
In ΔODB, we get,
∠OBD + ∠ODB + ∠BOD = 180°
55° + 45° + ∠DOB = 180° (using 1)
∠BOD = 180 °- 100°
∠BOD = 80°
Thus,∠BOD = 80°
APPEARS IN
संबंधित प्रश्न
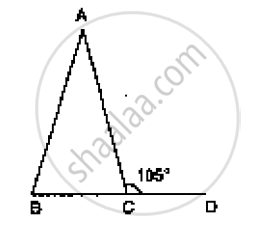
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Prove that each angle of an equilateral triangle is 60°.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
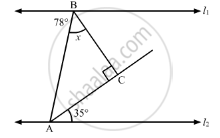
In the given figure, for which value of x is l1 || l2?
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
