Advertisements
Advertisements
Question
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
Options
100°
80°
90°
135°
Solution
In the given problem, line segment AB and CD intersect at O, such that ,AC || DB , ∠CAB = 45° and ∠CDB = 55° .
We need to find ∠BOD

As AC || DB
Applying the property, “alternate interior angles are equal”, we get,
∠OBD = ∠CAB
∠OBD= 55° .......(1)
Now, using the angle sum property of the triangle
In ΔODB, we get,
∠OBD + ∠ODB + ∠BOD = 180°
55° + 45° + ∠DOB = 180° (using 1)
∠BOD = 180 °- 100°
∠BOD = 80°
Thus,∠BOD = 80°
APPEARS IN
RELATED QUESTIONS
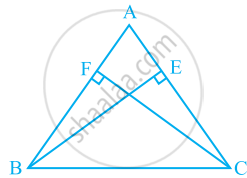
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
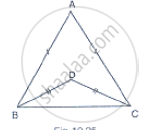
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
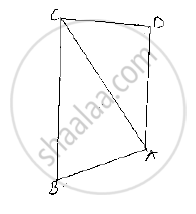
In Fig. 10.131, prove that: (i) CD + DA + AB + BC > 2AC (ii) CD + DA + AB > BC
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
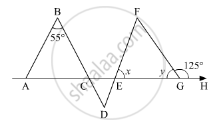
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
