Advertisements
Advertisements
Question
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
Options
60°
120°
150°
30°
Solution
In the given ΔABC,∠A = 60° and ∠B = 80° . Bisectors of ∠B and ∠C meet at O.
We need to find ∠BOC
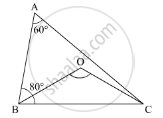
Since, OB is the bisector of ∠B.
Thus, `∠OBC = 1/2 ∠ABC ..... (1)`
Now, using the angle sum property of the triangle
In ΔABC, we get,
∠A + ∠B + ∠C =180°
60° + 80° + ∠C = 180°
140° + ∠C = 180°
∠C = 180° - 140°
∠C = 40°
Similarly, in ΔBOC
∠OBC + ∠O + ∠OCB = 180
∠O + 20° + 40°=180°
∠O + 60° = 180°
∠O = 180° - 60°
= 120°
Hence, ∠BOC = 120°
APPEARS IN
RELATED QUESTIONS
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
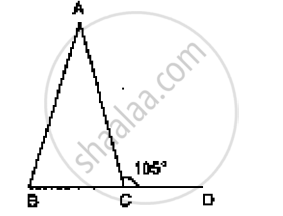
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
