Advertisements
Advertisements
Question
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Solution
False (F)
Reason: Since two sides are equal, the triangle is an isosceles triangle.
⇒ The two altitudes corresponding to two equal sides must be equal.
APPEARS IN
RELATED QUESTIONS
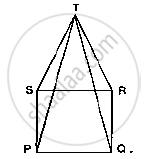
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Fill the blank in the following so that the following statement is true.
Angle opposite to equal sides of a triangle are .....
Write the sum of the angles of an obtuse triangle.
In ΔABC, if ∠A = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B =
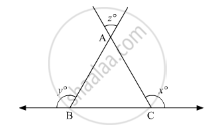
In the given figure, what is z in terms of x and y?
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
Which of the following correctly describes the given triangle?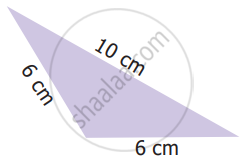
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
