Advertisements
Advertisements
Question
Write the sum of the angles of an obtuse triangle.
Solution
In the given problem, ΔABC is an obtuse triangle, with ∠B as the obtuse angle.

So, according to “the angle sum property of the triangle”, for any kind of triangle, the sum of its angles is 180°. So,
∠A+ ∠B + ∠C = 180°
Therefore, sum of the angles of an obtuse triangle is 180°.
APPEARS IN
RELATED QUESTIONS
Show that the angles of an equilateral triangle are 60° each.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
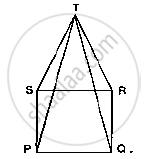
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
In a ΔABC, if ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O, then ∠BOC =
In the given figure, for which value of x is l1 || l2?
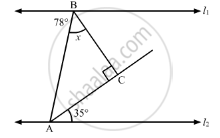
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
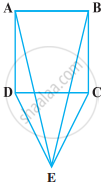
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
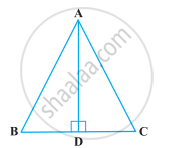
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
