Advertisements
Advertisements
Question
In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
Solution
In ΔABC, ∠B = 60, ∠C = 80 and the bisectors of ∠B and ∠C meet at O.
We need to find the measure of ∠BOC
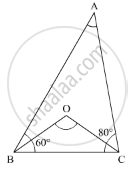
Since,BO is the bisector of ∠B
∠OBC = 1/2 ∠B
`= 1/2 (60°)`
= 30°
Similarly,CO is the bisector of ∠C
`∠OCB 1/2 ∠C`
= 1/2(80°)
= 40°
Now, applying angle sum property of the triangle, in ΔBOC, we get,
∠OCB + ∠OBC + ∠BOC = 180°
30° + 40° + ∠BOC = 180°
∠BOC + 70° = 180°
∠BOC = 180°- 70°
= 110°
Therefore, ∠BOC = 110°.
APPEARS IN
RELATED QUESTIONS
Can a triangle have All angles less than 60° Justify your answer in case.
Can a triangle have All angles equal to 60°? Justify your answer in case.
Is the following statement true and false :
A triangle can have two right angles.
Is the following statement true and false :
An exterior angle of a triangle is less than either of its interior opposite angles.
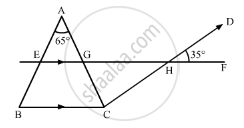
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
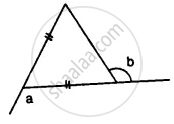
In the given figure, express a in terms of b.
Can 30°, 60° and 90° be the angles of a triangle?
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.
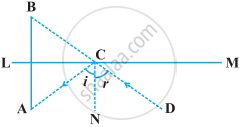
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].