Advertisements
Advertisements
प्रश्न
In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
उत्तर
In ΔABC, ∠B = 60, ∠C = 80 and the bisectors of ∠B and ∠C meet at O.
We need to find the measure of ∠BOC
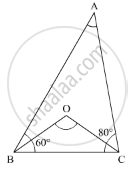
Since,BO is the bisector of ∠B
∠OBC = 1/2 ∠B
`= 1/2 (60°)`
= 30°
Similarly,CO is the bisector of ∠C
`∠OCB 1/2 ∠C`
= 1/2(80°)
= 40°
Now, applying angle sum property of the triangle, in ΔBOC, we get,
∠OCB + ∠OBC + ∠BOC = 180°
30° + 40° + ∠BOC = 180°
∠BOC + 70° = 180°
∠BOC = 180°- 70°
= 110°
Therefore, ∠BOC = 110°.
APPEARS IN
संबंधित प्रश्न
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
Fill in the blank to make the following statement true:
A triangle cannot have more than ...... right angles.
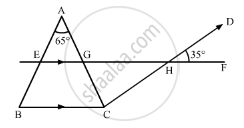
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
One of the base angles of an isosceles triangle is 52°. Find its angle of the vertex.
Find x, if the angles of a triangle is:
x°, 2x°, 2x°
One angle of a right-angled triangle is 70°. Find the other acute angle.
Classify the following triangle according to sides:
The correct statement out of the following is 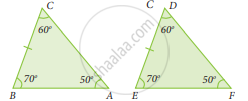
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
