Advertisements
Advertisements
प्रश्न
In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
उत्तर
In ΔABC, ∠B = 60, ∠C = 80 and the bisectors of ∠B and ∠C meet at O.
We need to find the measure of ∠BOC
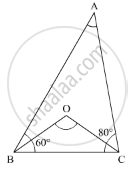
Since,BO is the bisector of ∠B
∠OBC = 1/2 ∠B
`= 1/2 (60°)`
= 30°
Similarly,CO is the bisector of ∠C
`∠OCB 1/2 ∠C`
= 1/2(80°)
= 40°
Now, applying angle sum property of the triangle, in ΔBOC, we get,
∠OCB + ∠OBC + ∠BOC = 180°
30° + 40° + ∠BOC = 180°
∠BOC + 70° = 180°
∠BOC = 180°- 70°
= 110°
Therefore, ∠BOC = 110°.
APPEARS IN
संबंधित प्रश्न
Compute the value of x in the following figure:
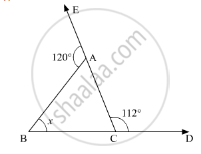
Compute the value of x in the following figure:
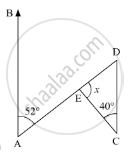
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
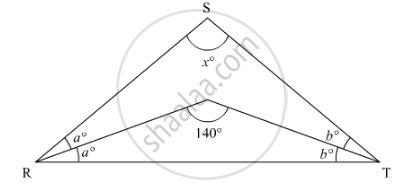
In ΔRST (See figure), what is the value of x?
Calculate the unknown marked angles of the following figure :
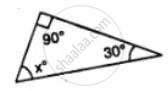
In the following, find the marked unknown angle:

One angle of a right-angled triangle is 70°. Find the other acute angle.
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.
