Advertisements
Advertisements
प्रश्न
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
उत्तर
In the given ΔABC, AD bisects ∠Aand ∠C >∠B. We need to prove ∠ADB >∠ADC.
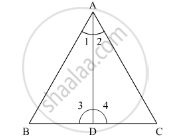
Let,
∠BAD = ∠1
∠DAC = ∠2
∠ADB = ∠3
∠ADC = ∠4
Also,
As AD bisects ∠A,
∠1 = ∠2…..(1)
Now, in ΔABD, using exterior angle theorem, we get,
∠4 = ∠B + ∠1
Similarly,
∠3 = ∠2 + ∠C
∠3 = ∠1 + ∠C [using (1)]
Further, it is given,
∠C >∠B
Adding ∠1to both the sides
∠C +∠1 >∠B + ∠1
∠3 > ∠4
Thus, ∠3 > ∠4
Hence proved.
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are arranged in ascending order of magnitude. If the difference
between two consecutive angles is 10°, find the three angles.
Can a triangle have two right angles? Justify your answer in case.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
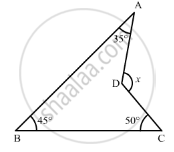
In the given figure, compute the value of x.
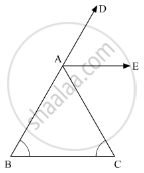
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
If two acute angles of a right triangle are equal, then each acute is equal to
State, if the triangle is possible with the following angles :
40°, 130°, and 20°
The length of the sides of the triangle is given. Say what types of triangles they are 4.3 cm, 4.3 cm, 4.3 cm.
D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
