Advertisements
Advertisements
प्रश्न
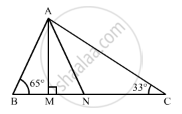
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
उत्तर
In the given ΔABC, AM⊥BC, ANis the bisector of ∠A, ∠B = 65 and ∠C = 33
We need to find ∠MAN
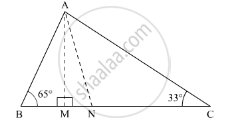
Now, using the angle sum property of the triangle
In ΔAMC, we get,
∠MAC + ∠AMC + ∠ACM = 180°
∠MAC + 90° + 33° = 180°
∠MAC + 123° = 180
∠MAC= 180° - 123°
∠MAC = 57°…….(1)
Similarly,
In ΔABM, we get,
∠ABM + ∠AMB+ ∠BAM = 180°
∠BAM + 90°+ 65° = 180°
∠AM + 155° = 180°
∠BAM = 180° - 155°
∠BAM …..(2)
So, adding (1) and (2)
∠BAM + ∠MAC = 25° + 57°
∠BAM + ∠MAC = 82°
Now, since AN is the bisector of ∠A
∠BAN = ∠NAC
Thus,
∠BAN + ∠NAC = 82°
2∠BAN =82°
` ∠BAN = (82°)/2`
= 41
Now,
∠MAN = ∠BAN - ∠BAM
= 41 - 25
= 16
Therefore, ∠MAN = 16.
APPEARS IN
संबंधित प्रश्न
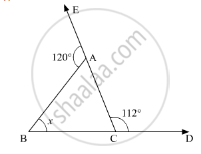
Compute the value of x in the following figure:
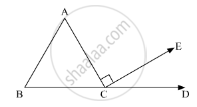
In the given figure, AC ⊥ CE and ∠A : ∠B : ∠C = 3 : 2 : 1, find the value of ∠ECD.
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
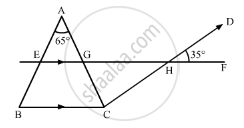
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
An exterior angle of a triangle is 108° and its interior opposite angles are in the ratio 4 : 5. The angles of the triangle are
Find the unknown marked angles in the given figure:
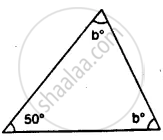
Find x, if the angles of a triangle is:
2x°, 4x°, 6x°
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
The length of the sides of the triangle is given. Say what types of triangles they are 3.4 cm, 3.4 cm, 5 cm.
