Advertisements
Advertisements
प्रश्न
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
उत्तर
In the given ΔABC, the bisectors of ext,∠B and ∠Cntersect at D
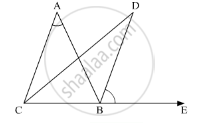
We need to prove: `∠D = 1/2 ∠A`
Now, using the exterior angle theorem,
\[\angle ABE = \angle BAC + \angle ACB\] .….(1)
\[As \angle \text {ABE and } \angle \text { ACB are bisected }\]
\[\angle DCB = \frac{1}{2}\angle ACB\]
Also,
\[\angle DBA = \frac{1}{2}\angle ABE\]
Further, applying angle sum property of the triangle
In ΔDCB
\[\angle CDB + \angle DCB + \angle CBD = 180^\circ\]
\[ \Rightarrow \angle CDB + \frac{1}{2}\angle ACB + \left( \angle DBA + \angle ABC \right) = 180^\circ\]
\[\angle CDB + \frac{1}{2}\angle ACB + \left( \frac{1}{2}\angle ABE + \angle ABC \right) = 180^\circ . . . . . \left( 2 \right)\]
Also, CBE is a straight line, So, using linear pair property
\[\Rightarrow \angle ABC + \angle ABE = 180^\circ\]
\[ \Rightarrow \angle ABC + \frac{1}{2}\angle ABE + \frac{1}{2}\angle ABE = 180^\circ \]
\[ \Rightarrow \angle ABC + \frac{1}{2}\angle ABE = 180^\circ - \frac{1}{2}\angle ABE . . . . . \left( 3 \right)\]
So, using (3) in (2)
\[\angle CDB + \frac{1}{2}\angle ACB + \left( 180^\circ - \frac{1}{2}\angle ABE \right) = 180^\circ \]
\[ \Rightarrow \angle CDB + \frac{1}{2}\angle ACB - \frac{1}{2}\angle ABE = 0\]
\[ \Rightarrow \angle CDB = \frac{1}{2}\left( \angle ABE - \angle ACB \right)\]
\[ \Rightarrow \angle CDB = \frac{1}{2}\angle CAB\]
\[ \Rightarrow \angle D = \frac{1}{2}\angle A\]
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
- ΔABE ≅ ΔACF
- AB = AC, i.e., ABC is an isosceles triangle.

Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Which of the following statements are true (T) and which are false (F):
The measure of each angle of an equilateral triangle is 60°
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Fill the blank in the following so that the following statement is true.
Sides opposite to equal angles of a triangle are ......
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
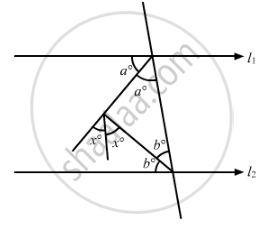
In the given figure, if l1 || l2, the value of x is
In ∆PQR, if ∠R > ∠Q, then ______.
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
