Advertisements
Advertisements
प्रश्न
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
उत्तर
False (F)
Reason: Since two sides are equal, the triangle is an isosceles triangle.
⇒ The two altitudes corresponding to two equal sides must be equal.
APPEARS IN
संबंधित प्रश्न
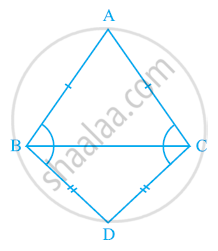
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Find the measure of each exterior angle of an equilateral triangle.
Which of the following statements are true (T) and which are false (F):
Sides opposite to equal angles of a triangle may be unequal
Which of the following statements are true (T) and which are false (F):
Angles opposite to equal sides of a triangle are equal
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
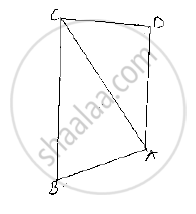
In Fig. 10.131, prove that: (i) CD + DA + AB + BC > 2AC (ii) CD + DA + AB > BC
Fill in the blank to make the following statement true.
If two angles of a triangle are unequal, then the smaller angle has the........ side opposite to it.
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
