Advertisements
Advertisements
प्रश्न
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
पर्याय
40°
50°
80°
130°
उत्तर
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to 50°.
Explanation:
According to the question, triangle ABC is: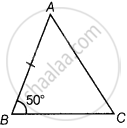
AB = AC ...[Given]
So, ∠C = ∠B ...[Angles opposite to equal sides are equal]
Given: ∠B = 50°
So, ∠C = 50°
APPEARS IN
संबंधित प्रश्न
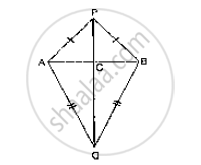
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
In the given figure, AB and CD are parallel lines and transversal EF intersects them at Pand Q respectively. If ∠APR = 25°, ∠RQC = 30° and ∠CQF = 65°, then

In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.
M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
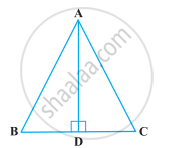
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
