Advertisements
Advertisements
प्रश्न
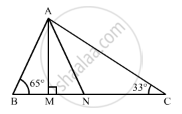
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
उत्तर
In the given ΔABC, AM⊥BC, ANis the bisector of ∠A, ∠B = 65 and ∠C = 33
We need to find ∠MAN
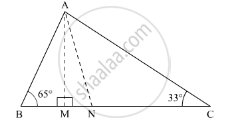
Now, using the angle sum property of the triangle
In ΔAMC, we get,
∠MAC + ∠AMC + ∠ACM = 180°
∠MAC + 90° + 33° = 180°
∠MAC + 123° = 180
∠MAC= 180° - 123°
∠MAC = 57°…….(1)
Similarly,
In ΔABM, we get,
∠ABM + ∠AMB+ ∠BAM = 180°
∠BAM + 90°+ 65° = 180°
∠AM + 155° = 180°
∠BAM = 180° - 155°
∠BAM …..(2)
So, adding (1) and (2)
∠BAM + ∠MAC = 25° + 57°
∠BAM + ∠MAC = 82°
Now, since AN is the bisector of ∠A
∠BAN = ∠NAC
Thus,
∠BAN + ∠NAC = 82°
2∠BAN =82°
` ∠BAN = (82°)/2`
= 41
Now,
∠MAN = ∠BAN - ∠BAM
= 41 - 25
= 16
Therefore, ∠MAN = 16.
APPEARS IN
संबंधित प्रश्न
Can a triangle have All angles more than 60°? Justify your answer in case.
Is the following statement true and false :
Sum of the three angles of a triangle is 180 .
Is the following statement true and false :
A triangle can have at most one obtuse angles.
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
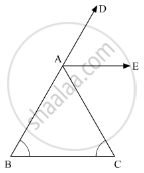
Find the value of the angle in the given figure:

Can a triangle together have the following angles?
55°, 55° and 80°
Can a triangle together have the following angles?
33°, 74° and 73°
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
9 cm, 6 cm, 16 cm
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
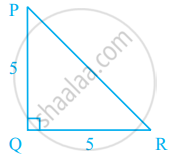
In figure, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm. Then ∆PQR is ______.